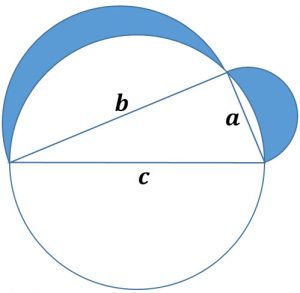
Given a right triangle with sides of length a, b, and c, first construct the circle whose diameter is the hypotenuse of length c. It is known from Euclidean Geometry that all three vertices of this triangle will lie on the circle. Next form the (outward facing) semicircles whose diameters are the legs of the triangle. The result is shown in the figure below. The shaded regions that lie outside of the big circle and inside the smaller circles are called lunes. Let L be the total area of the two lunes and let T be the area of the right triangle. Determine the value of L/T.
You must include work to support your result.