The area of the shaded region is $\pi$.
In our solution, we will first obtain a more general result where the chord of length 2 is replaced with an unspecified length $h$ which must of course be no bigger than the radius of the largest semicircle.
Let $a$, $b$, and $c$ be the radii of the semicircles in order of smallest to largest and let $\Delta = c-2a$ as shown in the figure below.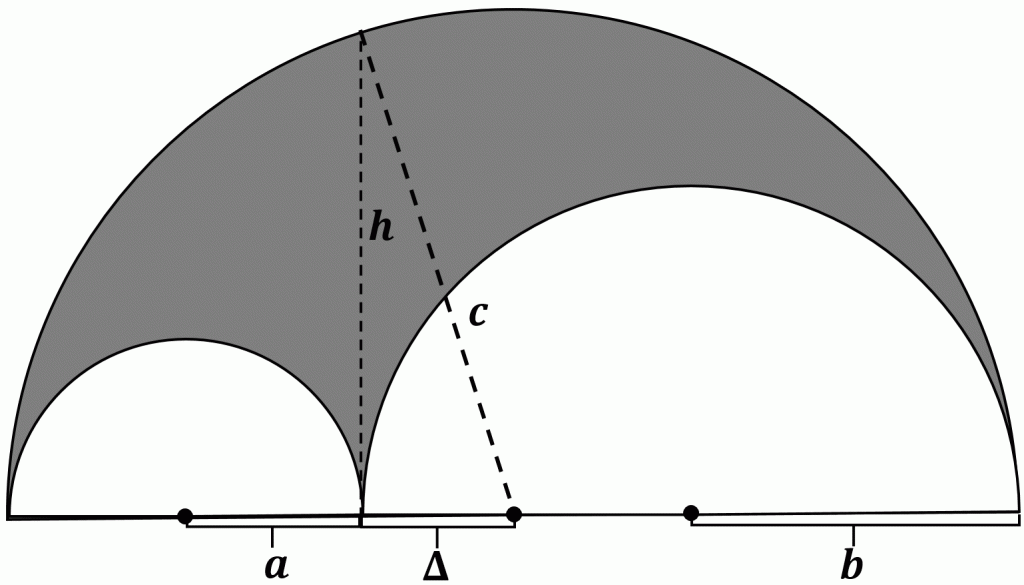
The area of the shaded region can be obtained by subtracting the areas of the two smaller semicircles from the area of the largest semicircle as follows:
$$A={1\over 2}\pi c^2 -{1\over 2}\pi a^2 -{1\over 2}\pi b^2 ={\pi\over 2}(c^2 -a^2-b^2) \tag{1}$$
Since the diameter of the largest semicircle is equal to the sum of the diameters of the smaller two semicircles, we have $2c=2a+2b$ or equivalently, $c=a+b$. Therefore,
$$c^2=(a+b)^2=a^2+2ab+b^2 \ \ \text{or equivalently,} \ \ c^2-a^2-b^2=2ab\tag{2}$$
Combining equations (1) and (2) we obtain
$$A={\pi\over 2}(c^2-a^2-b^2)={\pi\over 2}(2ab) \ \ \text{or simply} \ \ A=\pi ab \tag{3}$$
The radius of the largest circle is $c=2a+\Delta$ and therefore, $2a+\Delta=a+b$, or equivalently, $\Delta=b-a$. Using this result along with the Pythagorean Theorem gives us $c^2=\Delta^2+h^2=(b-a)^2+h^2=a^2 +b^2 -2ab+h^2$,
or simply
$$c^2-a^2-b^2=h^2-2ab \tag{4}$$
Combining equations (2) and (4) we find that
$$2ab=h^2-2ab\ \ \text{ or equivalently }\ \ ab={h^2\over 4}. \tag{5}$$
Finally we update the equation for the area of the shaded region given in (3) by substituting our result from (5) to obtain
$$A=\pi ab={\pi h^2 \over 4}$$
For the value $h=2$ given in the puzzler, we obtain that the area is ${\pi (2)^2\over 4}=\pi$.
