The answer is: 840 polar rectangles.
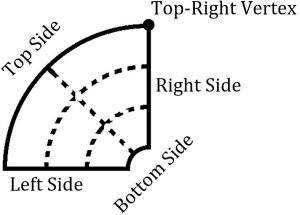
For the sake of the explanation, we will define the “bottom” side of a polar rectangle to be the side formed by the smaller of the two arcs and the “top” to be the side formed by the larger arc. With the polar rectangle oriented such that the top is facing up and the bottom is facing down, we define the left and right sides in the natural way. Furthermore, we define the top-right vertex of the polar rectangle to be the vertex where the top and right sides intersect. All other vertices are defined similarly. These definitions are illustrated in the diagram below.
Each polar rectangle in the grid can be uniquely determined by identifying the locations of its top-right vertex and bottom-left vertex. The only rules governing the selection of these two vertices are that they lie on different different circles and different radial lines. These selections can be made by carrying out the following steps:
- Select a radial line that the top-right vertex will lie on. For this step there will be 8 choices as there are 8 radial lines in the grid.
- Select a different radial line that the bottom-right vertex will lie on. For this step there will be 7 choices since we can not use the same radial line that was selected in the step 1.
- Select the two distinct circles that each of the vertices will lie on from among the 6 circles in the grid. With 6 circles to choose from, there are 15 different pairs of circles that we can select and the top-right vertex must lie on the circle with the bigger radius.
With 8 choices for our first step, 7 choices for our second step, and 15 choices for our third and final step, there are a total of 8(7)(15)=840 different ways to select locations for the top-right and bottom-left vertices and therefore 840 different polar rectangles in the grid.